Topological Data Analysis
Algebraic Topology
Algebraic topology is the study of topological spaces using abstract algebra.
Algebraic topology provides the language to classify topological spaces up to homeomorphism, that is, find the intrinsic qualitative aspects of spatial objects that remain invariant under homeomorphic transformations.
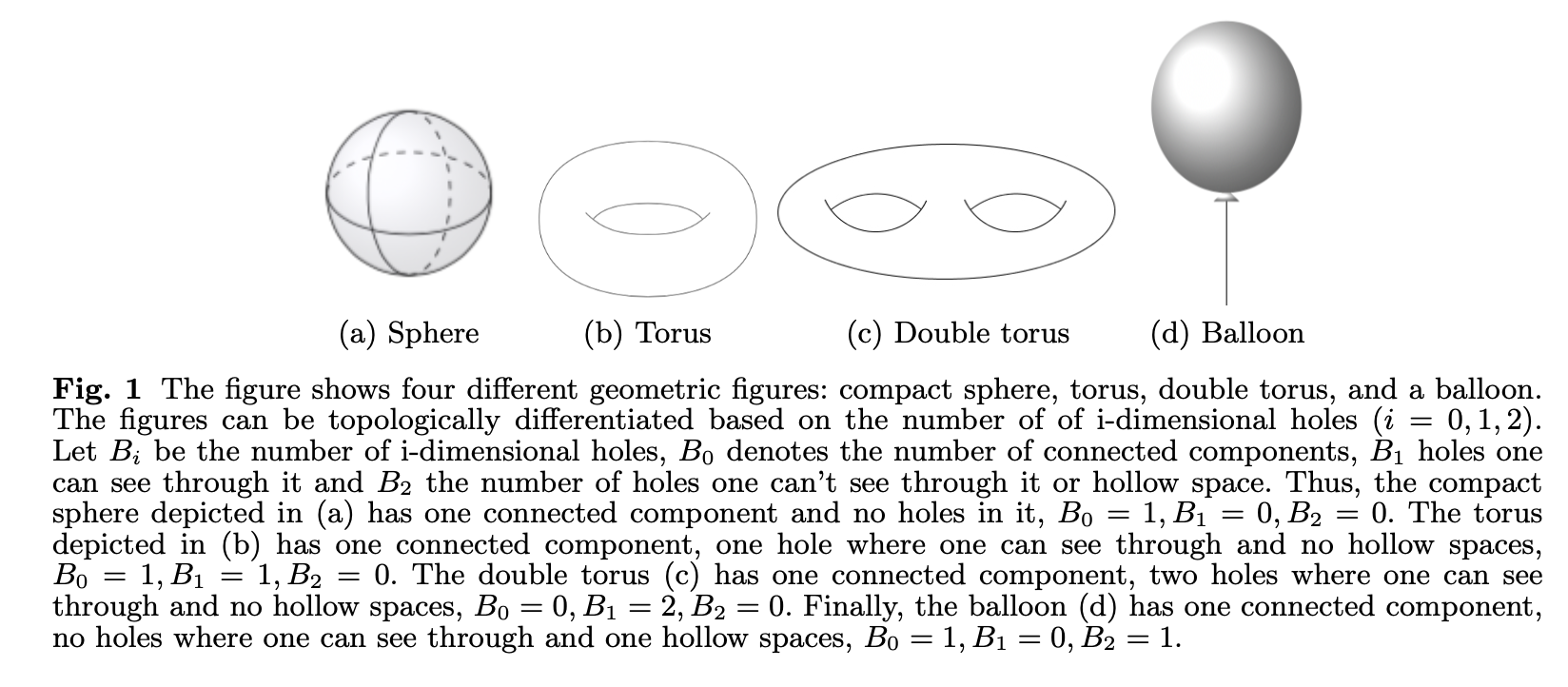
Topological Data Analysis
TDA provides a theoretical framework to extract data features taking into account the multiscale and multidensity of complex data sets. The goal of TDA is to apply topology to study qualitative features of data.
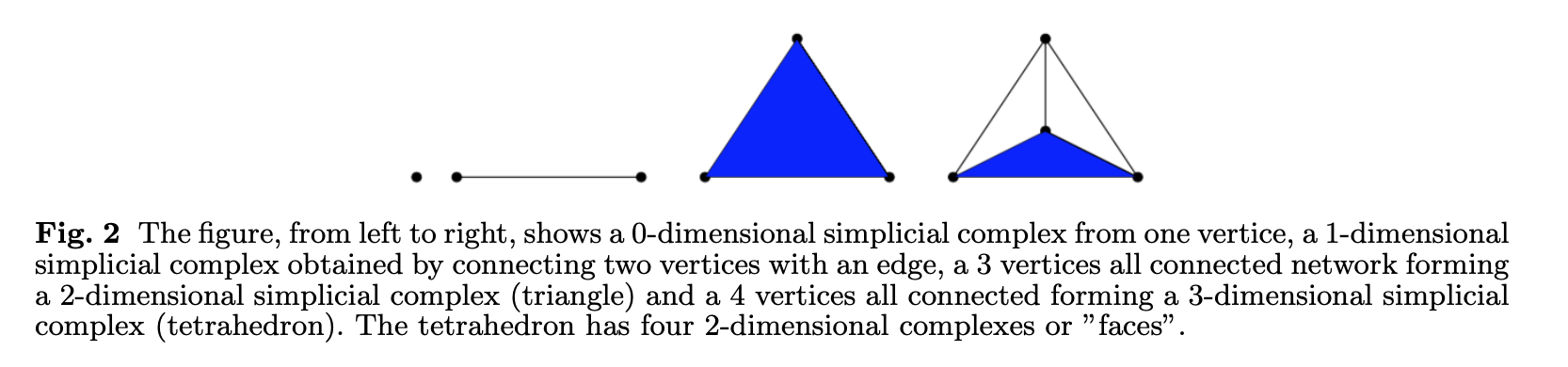
Basic Definitions
| Concept | Definition |
|---|---|
| Algebraic topology | The study of topological spaces using abstract algebra. |
| Topological space | T=(M,O) is an ordered pair or tuple consisting of a set M and a topology O. |
| Topology | For a given set M, a topology O is a subset of the power set of M such that: i. The empty set and the set M are in the topology O ii. For any two subsets of O, the intersection also exists in the topology O iii. The union of any subset of O also belongs to O |
| Simplicial Complex | A pair VX of vertices and SX of simplices. Each simplex in the set of simplices SX is a subset of the vertices VX plus the condition that if σ is in SX, then every subset τ ∈ σ also is in SX, τ ∈ SX. |
| Filtration | 1-parameter family of geometric objects, F(X) = {U(X,ε)},ε = {0,∞}, that is, a union of balls with varying radius. |
| Persistent Homology | A method used in topological data analysis (TDA) to study qualitative features of data that persist across multiple scales. It is robust to perturbations of input data and independent of dimensions and coordinates. |
Project’s description
The project aims to harness the power of Algebraic Topology and, more particularly, Topological Data Analysis (TDA) to characterize the relevant features in space and time of a dataset containing occurrences of crime in the city of Valencia, Spain.
Software
- GUDHI The GUDHI library is a generic open source C++ library, with a Python interface, for Topological Data Analysis (TDA) and Higher Dimensional Geometry Understanding. The library offers state-of-the-art data structures and algorithms to construct simplicial complexes and compute persistent homology.
- scikit-tda Scikit-TDA is a home for Topological Data Analysis Python libraries intended for non-topologists. This project aims to provide a curated library of TDA Python tools that are widely usable and easily approachable.
- Ripser Ripser is a lean C++ code for the computation of Vietoris–Rips persistence barcodes.
- Giotto-TDA A high-performance topological machine learning toolbox in Python
- rgdal Bindings for the ‘Geospatial’ Data Abstraction Library
Collaborators
- Jorge Mateu Mahiques (Universidad de Castellón, Spain